Triangle area calculator

Understanding the area of a triangle

The area of a triangle is a fundamental concept in geometry that represents the total space enclosed by its three sides. Understanding this concept is crucial because it allows us to quantify the size of triangular shapes, which are prevalent in various fields such as architecture, engineering, and art. The area of a triangle can vary significantly depending on its type—whether it's scalene, isosceles, or equilateral. Each type has unique properties that affect how we calculate its area. For instance, an equilateral triangle has all sides and angles equal, leading to a specific formula for its area calculation.

When discussing the area of triangles, it's essential to mention the units used to express this measurement. Typically, the area is expressed in square units like square meters (m²), square centimeters (cm²), or square inches (in²). These units help standardize measurements and make it easier to compare different triangles. Calculating the area of a triangle involves understanding these variations and applying appropriate formulas based on the given dimensions. Whether you're dealing with a right-angled triangle or an obtuse one, knowing how to compute its area accurately is invaluable. Here are some key points to consider:

• Scalene Triangle: All sides have different lengths, requiring specific calculations.
• Isosceles Triangle: Two sides are equal, simplifying some calculations.
• Equilateral Triangle: All sides and angles are equal, allowing for straightforward area computation.

Basic formula for calculating triangle area

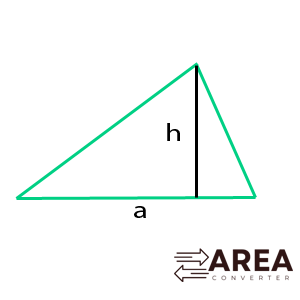
The basic formula for calculating the area of a triangle is straightforward and essential for anyone dealing with geometric shapes. This formula, A = 1/2 × base × height, allows you to determine the space enclosed by a triangle in a two-dimensional plane. The base refers to any side of the triangle, while the height is the perpendicular distance from the base to the opposite vertex. This method is applicable to all triangles, whether they are scalene, isosceles, or equilateral. Understanding this formula is crucial because it provides a foundation for more complex calculations involving triangles.

Let's look at some practical examples to see how this formula works in real-life scenarios:

• Example 1: If you have a triangle with a base of 10 inches and a height of 5 inches, the area would be calculated as follows: A = 1/2 × 10 × 5 = 25 square inches.
• Example 2: Consider a triangle with a base of 8 cm and a height of 7 cm. Using the formula, the area would be A = 1/2 × 8 × 7 = 28 square centimeters.

These examples illustrate how simple it can be to apply this formula once you know the base and height. By mastering this basic calculation, you'll be well-equipped to tackle more advanced problems involving triangles in various fields such as architecture and engineering.

Using Heron's formula for triangle area

Heron's formula is a powerful tool for calculating the area of a triangle when you know the lengths of all three sides. This method is particularly useful when the height of the triangle is not readily available, making it an essential technique in various mathematical and practical applications. To apply Heron's formula, you first need to determine the semi-perimeter of the triangle, which is half the sum of its three sides. The formula itself is expressed as:

• Step 1: Calculate the semi-perimeter (s) using the formula: \( s = \frac{a + b + c}{2} \), where \( a \), \( b \), and \( c \) are the lengths of the sides.
• Step 2: Use Heron's formula to find the area: \( \text{Area} = \sqrt{s(s-a)(s-b)(s-c)} \).

Let's consider an example to illustrate how Heron's formula works in practice. Suppose you have a triangle with side lengths of 7 cm, 8 cm, and 9 cm. First, calculate the semi-perimeter: \( s = \frac{7 + 8 + 9}{2} = 12 \). Then, substitute these values into Heron's formula to find the area:

• \( \text{Area} = \sqrt{12(12-7)(12-8)(12-9)} \)
• \( \text{Area} = \sqrt{12 \times 5 \times 4 \times 3} = \sqrt{720} = 26.83\) square centimeters.

This step-by-step approach ensures accuracy and provides a clear understanding of how Heron's formula can be applied effectively. Whether you're working on a geometry problem or tackling real-world challenges in fields like architecture or engineering, mastering this technique can be incredibly beneficial.

Calculating area with two Sides and an included angle

When you need to calculate the area of a triangle and you know two sides along with the included angle, there's a straightforward method to follow. This approach is particularly useful in scenarios where traditional base-height measurements are not available. The formula used in this case is derived from trigonometry and is expressed as: Area = 1/2 × side1 × side2 × sin(angle). Here, the angle is the one formed between the two known sides. This formula leverages the sine function to account for the angle's influence on the area, making it a versatile tool in geometry.

To illustrate this method, consider a triangle where side a measures 7 units, side b measures 9 units, and the included angle C is 30 degrees. Using our formula, we calculate: Area = 1/2 × 7 × 9 × sin(30°). Since sin(30°) equals 0.5, the area becomes 15.75 square units. This technique is not only efficient but also essential for various applications such as architecture and engineering, where precise measurements are crucial. Remember these key points when applying this method:

• The angle must be between the two known sides.
• The sine function is critical for accuracy.
• This formula adapts well to different triangle configurations.

Special cases: Right, equilateral, and isosceles triangles

When it comes to calculating the area of triangles, special cases like right-angled, equilateral, and isosceles triangles have their own unique formulas. Understanding these can simplify your calculations significantly. For a right-angled triangle, the formula is straightforward: the area is half the product of its base and height. This is because one of the sides acts as the height, making it easy to apply the basic formula. In contrast, an equilateral triangle, where all sides are equal, uses a different approach. The area is calculated using the formula: \(A = \frac{\sqrt{3}}{4} \times \text{side}^2\). This formula leverages the symmetry of equilateral triangles to provide a quick solution.

On the other hand, an isosceles triangle, which has two equal sides, requires another specific method. The area can be found using: \(A = \frac{1}{4}b\sqrt{4a^2 - b^2}\), where 'b' is the base and 'a' is one of the equal sides. Each type of triangle offers a unique way to calculate its area, reflecting its geometric properties. Here’s a quick summary:

By understanding these formulas, you can efficiently tackle problems involving these specific types of triangles in various practical scenarios.

Practical applications of triangle area calculation

Calculating the area of a triangle is not just an academic exercise; it has numerous practical applications across various fields. In architecture, understanding the area of triangular sections is crucial for designing roofs, facades, and other structural elements. Architects often use triangles to create aesthetically pleasing and structurally sound designs. Similarly, in engineering, triangles are fundamental in analyzing forces and stresses within structures. Engineers rely on precise calculations of triangular areas to ensure stability and safety in bridges, buildings, and other constructions.

Beyond architecture and engineering, the concept of triangle area finds its importance in several scientific disciplines. For instance, in geography, calculating the area of triangular plots can help in land surveying and mapping. In physics, understanding triangular areas can assist in determining vectors and forces acting at angles. Additionally, in environmental science, researchers might calculate the area of triangular sections of land to assess habitat sizes or resource distribution. These applications highlight how essential it is to grasp the concept of triangle area for practical problem-solving across diverse fields.

FAQ

What are some common mistakes to avoid when calculating the area of a triangle?

When calculating the area of a triangle, it's easy to make mistakes if you're not careful. One common error is using the wrong formula for the type of triangle you're dealing with. For instance, applying the formula for an equilateral triangle to a scalene one can lead to incorrect results. Another mistake is misidentifying the base and height, especially in right-angled triangles where one side acts as both. Additionally, forgetting to convert units or using inconsistent units throughout your calculations can also cause errors. Always double-check your measurements and ensure you're using the correct formula for the specific triangle type.

How does understanding the area of a triangle benefit professionals in various fields?

Understanding how to calculate the area of a triangle is incredibly useful across many professions. In architecture, it helps in designing structures with triangular elements like roofs and facades. Engineers use this knowledge to analyze forces and stresses within structures, ensuring stability and safety. In geography, calculating triangular areas aids in land surveying and mapping. Even in physics, understanding triangular areas assists in determining vectors and forces acting at angles. This knowledge is versatile and applicable in numerous practical scenarios.

Can you explain how Heron's formula differs from the basic area formula?

Heron's formula is particularly useful when you know all three sides of a triangle but not its height. Unlike the basic area formula (A = 1/2 × base × height), which requires knowing the base and height, Heron's formula allows you to calculate the area using just the side lengths. You first find the semi-perimeter (half of the perimeter) and then apply Heron's formula: Area = √[s(s-a)(s-b)(s-c)], where s is the semi-perimeter, and a, b, c are the side lengths. This method is handy when direct measurements of height aren't available.

What should I do if I only know two sides of a triangle but not any angles?

If you only know two sides of a triangle without any angles or additional information, you'll need more data to calculate its area directly. However, if you can determine or measure an included angle between those two sides, you can use the trigonometric formula: Area = 1/2 × side1 × side2 × sin(angle). Without an angle or additional information like another side length or height, calculating the exact area isn't possible.

Are there any real-world examples where calculating triangular areas is essential?

Absolutely! Calculating triangular areas is crucial in many real-world applications. For example, architects often design buildings with triangular sections for aesthetic appeal and structural integrity. Engineers might analyze triangular components within bridges or trusses to ensure they can withstand loads and stresses. In environmental science, researchers may calculate areas of triangular plots to study habitats or resource distribution efficiently.

How do I choose which side to use as the base when calculating a triangle's area?

The choice of which side to use as the base depends on convenience and available measurements. Typically, you'll choose a side that makes it easy to measure or calculate the corresponding height perpendicular to it. In right-angled triangles, one leg often serves as both base and height due to its perpendicular nature. For other triangles, select a base that simplifies finding or estimating its perpendicular height.

Why is it important to express triangle areas in square units?

Expressing triangle areas in square units standardizes measurements and facilitates comparison between different shapes or sizes. Square units like square meters (m²), square centimeters (cm²), or square inches (in²) provide consistency across calculations involving different dimensions or scales. This uniformity ensures clarity when communicating measurements across various fields such as architecture or engineering.